この記事はYahoo!ブログで公開していたもの[1]を元に作成されています。

一枚の正方形を別の正方形に分割することは、何も条件を付けなければ全く容易である。田形に切って４分割する、井桁の字に包丁目を入れて９分割する、あるいはその他の方法も含めて無限にあるだろう。

しかし「すべて異なる大きさの正方形で分割する」という付帯条件を付ければ、この種の問題は途端に難しくなる。隣接する正方形の大きさが異なれば、辺の差となる部分に段差が生じる。その部分を巧く埋めるように別の大きさの正方形を配置しなければならず、その方法も際限ないほど存在するように思えるからである。

1900年代前半の段階で、異なる大きさの正方形から成る長方形を見出すことはできていたが、正方形は一つも見つかっていなかった。モスクワ大学の教授 Lusin は、正方形を、いくつかの異なる大きさの正方形で分割することは不可能だと主張し、以後これは「Lusinの問題」として知られることになった。

ところが 1938年に入って69個の異なる正方形による解が見つかり、その翌年には更に少ない 55 個の解が見つかり、Lusin の主張は反証されることになった。[2]

用いる正方形の個数に制限をつけなければ、このような「完全正方形分割」が無限に存在することが明らかである。それはある解が見つかったとき、分割を構成している任意の正方形について、更に既に知られている別の完全正方形分割を施すことができるからである。辺の長さを整数にするには、全体を適当な倍率で拡大してやればよい。

したがって興味の対象は、できるだけ少ない個数の正方形から構成される解を求める点に向けられた。

1978年のこと、オランダの大学博士である Duijvestijn がコンピュータを用いて21個の解を見つけた。それは次の辺長を持つものである：

21個から成る解は（向きや裏返しなどを考慮しないで）本質的にただ一通りであり、21個未満の異なる解 - 完全正方形分割 - は存在しないことも証明されている。

正方形を異なる大きさの正方形で分割することが可能であると示されたのだが、立方体を異なる大きさの立方体で分割することは可能だろうか？
実は試みるまでもなく、これは不可能である。Wikipedia [3] に簡単な説明が付されている。

代わりに、無限平面を異なる大きさの正方形で分割することは可能である。Fibonacci 数列の値を辺の長さに持つ正方形を準備すればよい。そして中心から 1, 1, 2, 3, 5, ‥ の順番に渦巻きを成すように正方形を配置する作業を無限に続けていけば、平面上のいかなる点でもいつかはどれかの正方形の中に属することになる。

このとき、中央に辺の長さが１の正方形が２つ生成されてしまうからこのままでは題意に合わない。しかし既に Duijvestijn の与えた最小解をはじめとして、無数の完全正方形分割が知られているので、辺の長さが１の正方形のうちどちらか一つに適当な完全正方形分割を施せば、すべての正方形サイズが異なるように出来る。

正方形の部分を正多角形に置き換え、同種の問題を考えることはできないだろうか？

平面を埋め尽くすことが可能な正多角形の候補は、正三角形・正方形・正六角形に限られる。このうち「すべて異なる大きさ」という付帯条件を盛り込めば、明らかに正六角形では不可能であると分かる。異なる大きさの正六角形が隣接した場合、60度の鋭角部分が生じてしまうが、この部分は他のいかなる正六角形を用いても埋めることができないことは明らかだからだ。

正三角形の場合は厳密に確認していないが、まず不可能な感触がする。極めて大雑把な説明になるが、与えられた正三角形の内部に配置する一枚目の正三角形は、当然これより小さなサイズのものになる。次に、一枚目の正三角形に隣接する正三角形が必ず存在するのは自明だが、正三角形分割のルールより、一枚目の正三角形と辺の長さが同じであってはならない。必然的に一枚目より小さな正三角形となる。

この２個の正三角形を配置した時点で、与えられた正三角形の辺、一枚目と二枚目の正三角形の辺から六角形の３辺に相当する120度の角度を持つ折れ線が形成されるだろう。ここを埋めようとする過程でどうしても既に使ったのと同じ正三角形を用いざるを得なくなるか、さもなければ細長い溝状の領域が発生して、無限に小さくなる正三角形を無限個使わなければならない事態に陥ってしまうのである。これは分割の方法が悪いのではなく、本質的に「不可能である」という点に原因があるように思える。

これ以上の情報は以下のサイト[2]か、あるいは M. Lines の書籍に詳しい。（この記事も Malcolm E.Lines の書籍を一部参考にして書いている）

21枚の完全正方形分割については、学生の頃に実際に厚紙を切ったモデルを製作している。この記事の冒頭に貼られている配置図を見ないで、21枚の正方形の板を与えられた状態からスタートして、一枚の正方形を作るのは、かなり頭を使うパズルとなる。私が最初に21枚の解を知った書籍には、構成される正方形のサイズしか掲載されておらず、自力で組み上げるまで45分かかった。

家庭教師をしていたので、幾人か生徒に解かせてみたことがある。多くの生徒は（そして生徒の母親も）ギブアップしたのだが、たった一人30分で組み上げた猛者がいた。彼は今頃どうしているのだろうか？
完全正方形分割を知ったのは、末尾にある M.Lines の書籍が初めてであった。ルジンの問題を知ったのは更にその後で Wikipedia を参照してからだった。時系列としては最初に見つかったのはこれより若干サイズが大きいものであった。

末尾にあるように、学生時代にこのモデルを製作した。当時はジグソーパズルに凝っていてパズルの箱が丈夫な厚紙だったのでそれを利用している。当時造られた現物を今も持っている。

巡回家庭教師では英語と数学を教えていたので、数学的思考と遊びを兼ねてあちこちの生徒宅へ持参した。生徒ばかりでなく親も一緒に考えた家庭もあった。半数くらいの生徒が分からないとギブアップしたが、厚南中原に居た中学生のある生徒は30分で解き、組み上げた見取り図を見せてくれた。そして家の方も「本当に30分くらいで解いていたんですよ」と言っておられたのを覚えている。

この移植記事を作成するにあたって押し入れから現物を取り出し上記の写真を撮影した。このようなシンプルな学習教材を製作することは当時から考えていたが、現在も巡回家庭教師を続けているばかりでなく校区の小学生たちを相手に新しい種の教育に携わろうとしている。丈夫なカラーの画用紙を買ってきて数セット作り、パズルとして広めようかと考えている。
Lusinは異なる大きさの正方形分割は不可能であると予想していた。実際は不可能どころかそのような分割が無限に存在していたのだが、何のヒントも与えられないままこの問題を出題されたなら、殆どの人が「できない」と答えるのではないだろうか。実際自分もそう思っていたし、それ故にこの問題を考えることもなかった。

用いる正方形の個数に制限を設けないなら、一つの解が得られたならそれを元に無数に作ることができる。解を構成する正方形のうちの一つに、自身を縮小した正方形配置を埋め込むことができるからである。それは構成要素のどの正方形でもよく、更にいくつ埋め込んでも構わない。[4]したがって n 枚の異なる正方形で構成される本質的な完全正方形分割の個数を f(n) とすると、f(n) は単調増加関数でありしかもかなり大きな速さで発散する。上記の結果より f(21) = 1 と k<21 の正の整数に対して f(k) = 0 が確定している。

n を固定したとき、完全正方形を構成する各正方形の辺の長さに着目することもできる。たとえば辺の長さが１であるものを含む完全正方形に課せられる条件とか、できるだけ長い連続した整数を辺の長さに持つ解を探すとかである。予想としてはどれだけ長い連続した整数辺の完全正方形でも存在可能だろう。
（しかし１から始まる連続した整数辺のみで構成される完全正方形は存在しない[5]）

空間の完全立方体分割が不可能であることは記事に書いた。平面を埋め尽くす正多角形は他に正三角形と正六角形があり、記事では断定していないが、そのどちらを用いた場合でも有限な領域に対する完全正三角形（正六角形）分割は不可能である。殊に正六角形で不可能であることはかなり自明である。

正六角形はすべての頂角が120度である。辺長が同じもの（即ち合同な正六角形）を接し合わせたときに限り接点部分に120度の角度が生じ、そこへ同じ正六角形を配置することで平面を埋め続けることができる。しかし辺長が異なる正六角形を接し合わせると60度の角が生じてしまい３枚目の正六角形を配置できなくなる。したがって「すべて異なる辺長」という条件では、完全正六角形分割どころか単純に平面を埋め尽くすことさえ不可能である。

正三角形の場合は異なる辺長を接し合わせて120度の角度が発生するので、そこに異なる２枚の正三角形を置くことで埋めることができそうに見える。しかし題意から正三角形の内部を埋め尽くさなければならないので、完成形となる正三角形の縁が存在する。異なる辺長の正三角形を使い続ける限り、どう配置しても条件を満たしつつ埋めることができなくなる「溝状領域」が発生してしまう。

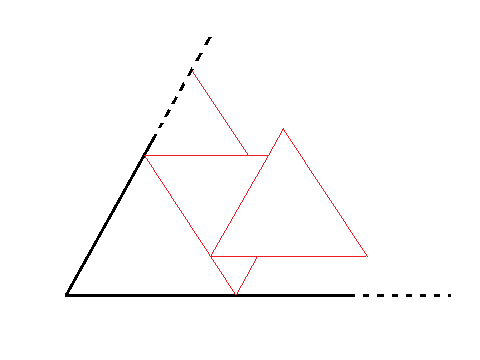
この溝を埋めるなら同じサイズの正三角形が要求され、さもなければサイズを縮小し続けながら配置する堂々巡りに陥ることになる。60度と120度という異なる角度が生じることにより溝状領域が生じるのが原因である。外側の縁に制限がなければ辺長を増やしつつ埋め続けることが可能というだけで、有限な正三角形を完全分割することはできないことが分かる。

完全な正方形分割が可能なのに正三角形と正六角形では不可能なのは、構成要素の辺を接したときに生じる角度が正方形のように一つ（即ち常に直角）に定まらないのが本質的原因である。

ホームに戻る