この記事はYahoo!ブログで公開していたものを元に作成されています。

k * 2ⁿ + 1 の形の数において、どんな正の整数 n に関しても常に合成数を与えるような奇数 k を Sierpinski Number [1]と定義するのであった。
そのような k は紛れもなく存在するのであるが、逆に n を固定して k を動かした場合、どんな n に対しても常に合成数を与えるようには出来ない。即ち、どんな n に対しても必ず値が素数となるようなk が無限に存在する。（これは Dirichlet の算術級数の定理から明らか）

したがって n を与えれば、最小素数を与える k が必ず存在する。そのときの k は n に対してどんな振る舞いをするだろうか図式化したのがこのグラフである。

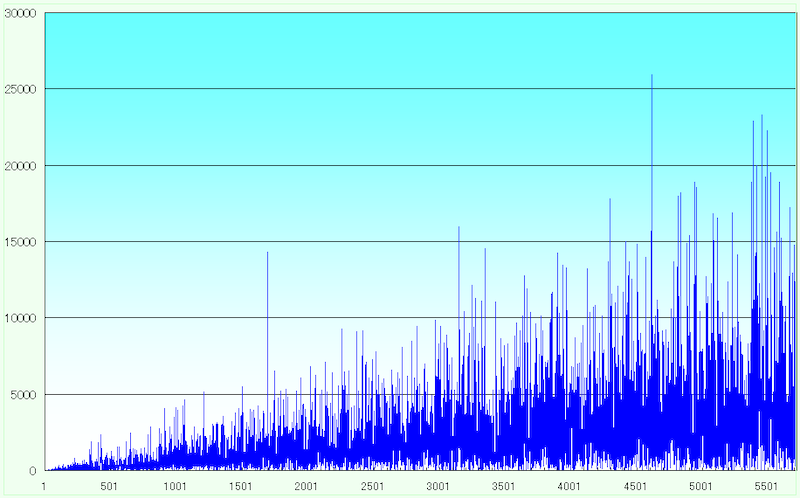
絶対値が大きくなるにつれて素数の密度は希薄になっていくから、n が大きくなるにつれて最小素数は次第に大きくなると考えられる。つまり k の値も上昇すると予測される。

グラフは非常にギザギザした形状を示している。n = 1,700 付近に突出した値が見られるが、これはn = 1,695 のときの k = 14,319 に対応する。即ち k * 2¹⁶⁹⁵ + 1 が素数となる最小の k の値が 14,319 であることを示している。

全体的にはグラフの帯となる中心部分は、上下動を反復しながら少しずつ上昇しているように思われる。

些か乱暴であるが k と最小値を与える n を一次近似することを考えた。最小値を与える n の平均値を求めてそれを k で割った値を縦軸に取った推移が赤色のグラフである。

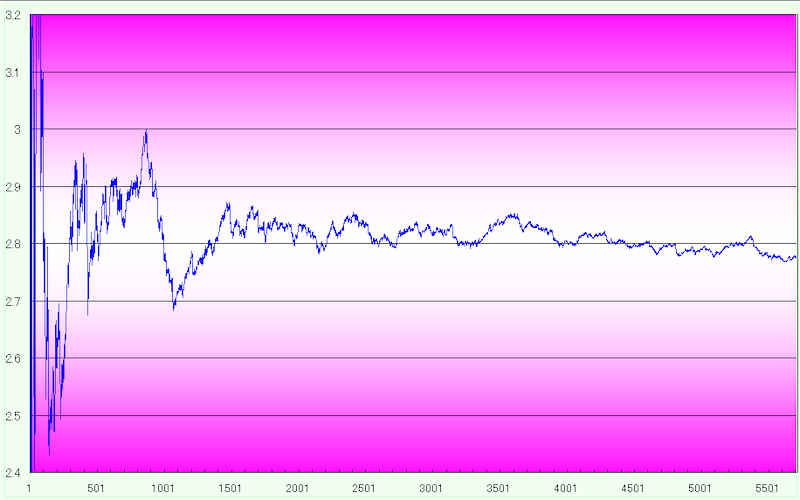
値 k が小さいうちは、変動が非常に激しい。荒い上下動を繰り返し、n が1,000 付近に達してもなお落ち着く気配がない。指数としては 1,000 程度だが、実際の数値は 300 桁を軽く超える大きさである。n が1,500 を超えたあたりからこの比は漸く変動が小さくなり、グラフを見る限り 2.8 付近のある値に収束しそうな気配である。

この比率が 2.8 付近に収束するか否かはもちろん、特定の値に収束するかどうかすら不明である。まだ調査範囲が広くはなく、もっと先に進んだところで 2.8 ラインから大きく外れるかも知れない。

この定数を仮定すれば、n が非常に大きい値を取る場合、k をどのあたりまで大きくすれば最小素数が得られるかの目安をたてることができる。例えば n = 28,000 付近の値を取った場合、k は平均的には10,000付近であるから、その値まで調べることによって素数を得るまでの平均時間が判明する。

しかし平均値が分かったところで、ある n に対して最小の素数を与える k がどう与えられるかには全く貢献しないのは、素数定理を元にした素数分布と同じである。

n に２の大きなベキ乗を取った場合で k の最小値を考えてみよう。
n = 16384 (2¹⁴) , n = 32768 (2¹⁵) , n = 65536 (2¹⁶) の場合では、それぞれこの順で k の最小値も大きくなると考えられる。しかし実際には最小素数は
が条件を満たす最小だから、全く予想に反する結果となっている。n = 65536 の場合、先の収束比を仮定すれば 65536 ÷ 2.8 ≒ 23400 だから k が２万項を超えて走査しなければ最小素数が見つからない可能性があると言える。実際は小さなところに最小素数が見つかったのは、全く幸運だったのだろう。

実際、この次のケースである n = 131072 では、k は20000 を超えて調査しているにも関わらず、なお最小素数が出力されて来ないのだった。
（後日の調査で、50655 * 2¹³¹⁰⁷² + 1 が最小素数であることが判った）
記事作成日と最終編集日から見てとれる通り、十数年前に書いたブログ記事をそのままここへ移植している。このため自分で書いたブログ記事ながらいろいろとツッコミどころがある。

上記テキストは Yahoo! ブログに公開していたものを Ameba ブログへ移植した後にテキストと画像データを当サイトへ移しただけの内容で、詳細説明なしで書き始めているのでタイトルだけでは何のことか分からない。当時は類似する記事を他にもいくつか書いているためにこのような省略したタイトルとなったようだ。

冒頭にある k * 2ⁿ + 1 という形の数（プロス数）は、その特異な形を利用して素数判定が比較的容易であり、判定ソフトをダウンロードして利用可能である。この Proth test を動かしていてブログのような問題を思い付いて演習している。Yahoo!ブログに公開していたのは冒頭のタグからこの項目の直前までの内容である。閲覧回数は不定であり、読者コメントは皆無だった。

現在の視点から改めて評議すべき点がいくつかある。k と n の挙動を直接視覚化したブルーのグラフは理解できるが、最小素数を与える k の平均値を調べる考え方は面白いものの、一次近似は乱暴な気がする。一連のグラフを作出した大元の表計算ファイル（Excelで作成していた）からグラフウィザードを用いてグラフ化している。大元のファイルでは確か最小素数を与える k を n ごとに求め、その総和を n で割っていたと思う。この平均値の算出手法の妥当性と、グラフの x 軸の目盛りの取り方に疑問がある。指数ないしは対数目盛にしなければグラフの挙動を窺い知ることができないかも知れない。

また、x の値が 5,000 程度の「小さすぎる」値から収束先を推測することは無謀である。記事で「2.8あたりに収束するのでは」と書いているのは、根拠もなく2√2が頭に浮かんだからだろう。有限な値に収束するのは確からしいが、それが既知の特に意味を持つ値（例えば自然対数の底など）に向かうとは限らない。

ちなみにこのグラフを作出する元となったデータは表計算ソフト（Excel）でファイル化していたのだが、どういう訳かバックアップ側のHDDにもこのファイルが存在しない。グラフ画像もブログ側へ移植したものしかない。バックアップ手順の誤りで削除されてしまったが、この記事を書いた後に起きたと推測されるHDDクラッシュ事件で喪われてしまった可能性がある。Ameba ブログが消失すると記事が何処にもなくなってしまうので、このたびテキストとグラフ画像をここへ移植した次第である。
この問題は、以下のような問いかけに焼き直すことができる。
ブログ記事では n を x 軸、k₁ を y 軸にプロットし、それぞれを折れ線で結んでグラフ化している。青い方は棒グラフのように見えるが、狭い間隔を500等分して表示しているからである。

グラフでは上方に突出したプロットが何度も生じている。しかし突拍子もなく上の方まで飛んでしまうような k は見当たらない。n の大きさによってその周辺の平均的な素数密度が定まるからであり、この意味では平均的なものであれば n に対する k の上界の近似式が導出できるかも知れない。

n が増加してもなお y 軸側に貼り付く点も多い。k = 1 が素数となる事例は Fermat 素数以外ない（殆ど間違いなく有限個）が、k = 3 が素数となるケースは無限に生じる可能性がある。これは 3 * 2ⁿ + 1 という形の素数が無限に存在するかどうかという問題に帰着される。恐らく Mersenne 素数と同じような結果（ほぼ確実に無限に存在する）となるだろう。

n を無限大に向かって動かしたときの k の平均値の挙動は、どのような平均値を採用するかにも依る。素朴な手法はブログ記事のようなΣ k₁ を n で除した値だが、どう考えてもブログ記事のような n が 5000 程度では挙動を観察するには小さすぎる。青のグラフを見ると上方に突出したピークが少なく青帯の上側に白い溝が生じている部分がいくつもある。これは連続的な n の増加に対して k₁が小さな値ばかり続くとき起きる現象である。こういった区間に出会うと平均値は下落し、逆に上方ピークが続けば上昇する。k₁ の値が１ケタから５ケタまで荒く変動するので、平均値が落ち着きを見せるには n を少なくとも10倍、できれば100倍以上にまで拡張しなければ傾向を観察することは出来ないだろう。
ブログを書いたのは十数年前であり、現在ではPCのスペックが当時よりもずっと上がっている。一連の計算と結果の表作成を自動化できれば、n のオーダーをもう１ケタ上げることは容易である。実際の演習では k₁ が求まった都度プログラムを停止し、n を一つ増やして再実行させていたような気がする。この場合、残念ながら１ケタ上のデータを得るために当時と同じことを実行するだけのメリットを感じない。

この他に可能な演習として、n を固定した場合に k₁ と n の比はどこまで大きくなれるかというものがある。単純な比だと”数の原始時代”である最初の方で上限と下限が定まってしまう可能性もあるので、関数比 f(n) / f(k₁) に置き換えても良い。冒頭の算術級数の定理より k₁ はすべての n に対してかならず有限な値に定まるから、比または関数比を解析することで「最悪でもこの大きさまでの k まで計算すれば素数が現れる」が言えるようになるかも知れない。

Proth test では k * 2ⁿ - 1 の形の数についても高速に素数判定できるので、符号をマイナスに変えた場合に同種の演習が可能である。その他に底を３や５に変えたり、n の重複性を避けるために k を奇数に限定することもできる。

ホームに戻る